Convolutional models have been widely used in multiple domains. However, most existing models only use local convolution, making the model unable to handle long-range dependency efficiently. Attention overcomes this problem by aggregating global information based
on the pair-wise attention score but also makes the computational complexity quadratic to
the sequence length. Recently, Gu et al. [2021a] proposed a model called S4 inspired by
the state space model. S4 can be efficiently implemented as a global convolutional model
whose kernel size equals the input sequence length. With Fast Fourier Transform, S4 can
model much longer sequences than Transformers and achieve significant gains over SoTA on
several long-range tasks. Despite its empirical success, S4 is involved. It requires sophisticated parameterization and initialization schemes that combine the wisdom from several
prior works. As a result, S4 is less intuitive and hard to use for researchers with limited
prior knowledge. Here we aim to demystify S4 and extract basic principles that contribute
to the success of S4 as a global convolutional model. We focus on the structure of the
convolution kernel and identify two critical but intuitive principles enjoyed by S4 that are
sufficient to make up an effective global convolutional model: 1) The parameterization of the
convolutional kernel needs to be efficient in the sense that the number of parameters should
scale sub-linearly with sequence length. 2) The kernel needs to satisfy a decaying structure
that the weights for convolving with closer neighbors are larger than the more distant ones.
Based on the two principles, we propose a simple yet effective convolutional model called
Structured Global Convolution (SGConv). SGConv exhibits strong empirical performance over
several tasks: 1) With faster speed, SGConv surpasses S4 on Long Range Arena and Speech
Command datasets. 2) When plugging SGConv into standard language and vision models,
it shows the potential to improve both efficiency and performance. Code is available at
GitHub - ctlllll/SGConv.
- The parameterization of the convolutional kernel needs to be efficient in the sense that the number of parameters should scale sub-linearly with sequence length.
- The kernel needs to satisfy a decaying structure that the weights for convolving with closer neighbors are larger than the more distant ones.
Based on the two principles, we propose a simple yet effective convolutional model called Structured Global Convolution (SGConv).
Handling Long-Range Dependency (LRD) is a key challenge in long-sequence modeling tasks
such as time-series forecasting, language modeling, and pixel-level image generation. Unfortunately, standard deep learning models fail to solve this problem for different reasons: Recurrent
Neural Network (RNN) suffers from vanishing gradient, Transformer has complexity quadratic in
the sequence length, and Convolutional Neural Network (CNN) usually only has a local receptive
field in each layer.
To answer these questions, we focus on the design of the global convolution kernel. We extract
two simple and intuitive principles that contribute to the success of the S4 kernel. The first
principle is that the parameterization of the global convolution kernel should be efficient in terms
of the sequence length: the number of parameters should scale slowly with the sequence length.
For example, classic CNNs use a fixed kernel size. S4 also uses a fixed number of parameters
to compute the convolution kernel while the number is greater than classic CNNs. Both models
satisfy the first principle as the number of parameters does not scale with input length. The
efficiency of parameterization is also necessary because the naive implementation of a global
convolution kernel with the size of sentence length is intractable for inputs with thousands of
tokens. Too many parameters will also cause overfitting, thus hurting the performance. The
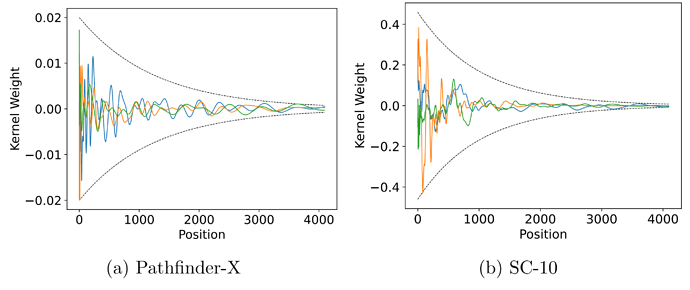
second principle is the decaying structure of the convolution kernel, meaning that the weights
for convolving with closer neighbors are larger than the more distant ones. This structure
appears ubiquitously in signal processing, with the well-known Gaussian filter as an example.
The intuition is clear that closer neighbors provide a more helpful signal. S4 inherently enjoys
2
this decaying property because of the exponential decay of the spectrum of matrix powers (See
Figure 2), and we find this inductive bias improves the model performance (See Section 4.1.2).
Efficient Transformers. The Transformer architecture [Vaswani et al., 2017] has been successful across a wide range of applications in machine learning. However, the computation
and memory complexity of Transformer scales quadratically with the input length, making it
intractable for modeling long-range interactions in very long sequences. Therefore, several efficient variants of Transformer model have been proposed recently to overcome this issue [Child
et al., 2019, Wang et al., 2020, Kitaev et al., 2019, Zaheer et al., 2020, Tay et al., 2020a, Peng
et al., 2021, Qin et al., 2021, Luo et al., 2021]. Nevertheless, few of these methods performed
well on benchmarks such as Long Range Arena [Tay et al., 2020b], SCROLLS [Shaham et al.,
3
2022], which require long-range modeling ability.